PERTEMUAN KE 6
PJJ Matematika Minat, Senin 06 September 2021
Semoga anda dalam keadaaan sehat selalu, tak lupa saya ingatkan selalu patuhi protokol kesehatan : Memakai masker, Menjaga jarak dan Mencuci tangan di air yang mengalir. agar kita dapat terhindar dari terjangkit Virus Covid-19 yang dimana Pandemi ini sudah kita lalui hampir 1 tahun lebih. Dikarenakan sekolah sedang dalam persiapan PTTM, persiapkan dirimu agar semuanya lancar.
Pada kesempatan kali ini saya akan membahas tentang menggambar grafik fungsi trigonometri:
Periode Fungsi Trigonometri
Fungsi f dengan wilayah R dikatakan periodik apabila ada bilangan 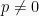 , sedemikian sehingga
, sedemikian sehingga  , dengan
, dengan 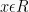 . Bilangan positif p terkecil yang memenuhi
. Bilangan positif p terkecil yang memenuhi  disebut periode dasar fungsi f.
disebut periode dasar fungsi f.
Jika fungsi f periodik dengan periode dasar p, maka periode-periode dari fungsi f adalah  , dengan n adalah bilangan asli. Jika f dan g adalah fungsi yang periodik dengan periode p, maka
, dengan n adalah bilangan asli. Jika f dan g adalah fungsi yang periodik dengan periode p, maka 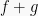 dan fg juga periodik dengan periode p.
dan fg juga periodik dengan periode p.
1. Periode fungsi sinus dan kosinus
Untuk penambahan panjang busur  dengan kelipatan
dengan kelipatan  (satu putran penuh) akan diperoleh titik p(a) yang sama, sehingga secara umum berlaku :
(satu putran penuh) akan diperoleh titik p(a) yang sama, sehingga secara umum berlaku :
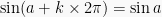 dengan k∈B atau
dengan k∈B atau dengan k∈B
dengan k∈B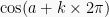 dengan k∈B atau
dengan k∈B atau dengan k∈B
dengan k∈B
Dengan demikian, fungsi sinus 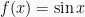 vatau
vatau  dan fungsi kosinus
dan fungsi kosinus  atau
atau  adalah fungsi periodik dengan periode dasar
adalah fungsi periodik dengan periode dasar  atau
atau  .
.

2. Periode fungsi tangen
Untuk penambahan panjang busur  dengan kelipatan
dengan kelipatan  (setengah putran penuh) akan diperoleh titik
(setengah putran penuh) akan diperoleh titik  yang nilai tangennya sama untuk kedua sudut tersebut, sehingga secara umum
yang nilai tangennya sama untuk kedua sudut tersebut, sehingga secara umum 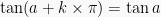 dengan
dengan  atau
atau  dengan
dengan  .
.

Dengan demikian tangen  atau
atau  adalah fungsi periodik dengan periode
adalah fungsi periodik dengan periode 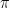 atau
atau  .
.
Grafik Fungsi Trigonometri

Dengan td adalah tidak didefinisikan. Untuk memudahkan, maka lihatlah segitiga berikut :

Dari konsep segitiga tersebut diperoleh nilai setiap sudut 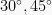 dan
dan  . Untuk sudut
. Untuk sudut  dan
dan  diperoleh dengan cara berikut :
diperoleh dengan cara berikut :

Didapat :
Jika titik 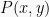 bergerak mendekati sumbu X positif, akhirnya berimpit dengan sumbu X, maka x=r, y=0,
bergerak mendekati sumbu X positif, akhirnya berimpit dengan sumbu X, maka x=r, y=0,  dan
dan 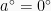 , sehingga
, sehingga
Jika titik P(x,y)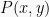 bergerak mendekati sumbu Y positif, akhirnya berimpit dengan sumbu Y, maka
bergerak mendekati sumbu Y positif, akhirnya berimpit dengan sumbu Y, maka
 , dan
, dan 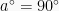 , sehingga
, sehingga

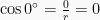
- tan
 = tidak didefinisikan
= tidak didefinisikan
Nilai Maksimum dan Minimum Fungsi Trigonometri
Untuk setiap titik P(x,y)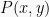 pada fungsi trigonometri memiliki hubungan :
pada fungsi trigonometri memiliki hubungan :
Berdasarkan uraian tersebut dapat dikemukakan bahwa :
Nilai maksimum dan minimum fungsi sinus
- Fungsi sinus
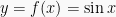 memiliki nilai maksimum
memiliki nilai maksimum  yang dicapai untuk
yang dicapai untuk  dengan
dengan  dan nilai minimum
dan nilai minimum  yang dicapai untuk
yang dicapai untuk  dengan
dengan  .
. - Fungsi sinus
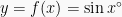 memiliki nilai maksimum
memiliki nilai maksimum  yang dicapai untuk
yang dicapai untuk  dengan
dengan  dan nilai minimum
dan nilai minimum 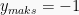 yang dicapai untuk
yang dicapai untuk 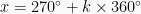 dengan
dengan  .
.
Nilai maksimum dan minimum fungsi kosinus
- Fungsi kosinus
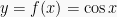 memiliki nilai maksimum
memiliki nilai maksimum  yang dicapai untuk
yang dicapai untuk 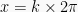 dengan
dengan  dan nilai minimum
dan nilai minimum  yang dicapai untuk
yang dicapai untuk  dengan
dengan  .
. - Fungsi kosinus
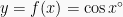 memiliki nilai maksimum
memiliki nilai maksimum  yang dicapai untuk
yang dicapai untuk  dengan
dengan  dan nilai minimum
dan nilai minimum  yang dicapai untuk
yang dicapai untuk  dengan
dengan  .
.
Secara umum dapat dikemukakan bahwa :
- Jika fungsi sinus
 , maka nilai maksimumnya
, maka nilai maksimumnya 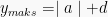 dan nilai minimumnya
dan nilai minimumnya 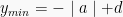
- Jika fungsi kosinus
 , maka nilai maksimumnya
, maka nilai maksimumnya 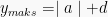 dan nilai minimumnya
dan nilai minimumnya 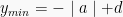
Jika 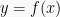 adalah fungsi periodik dengan nilai maksimum
adalah fungsi periodik dengan nilai maksimum 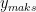 dan minimum
dan minimum  , maka amplitudonya adalah :
, maka amplitudonya adalah :

Jenis Grafik Fungsi Trigonometri
1. Grafik fungsi baku 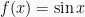 ;
;  ; dan
; dan 
Sinus

Kosinus

Tangen

2. Grafik fungsi 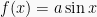 ;
;  ; dan
; dan 
Didapat dari grafik trigonometri baku dengan cara mengalikan koordinat setiap titik pada grafik baku dengan bilangan a, sedangkan absisnya tetap. Periode grafik tetap  untuk kosinus dan sinus. Sedangankan periode tangen
untuk kosinus dan sinus. Sedangankan periode tangen  .
.
Sinus
Misalkan  , maka grafiknya :
, maka grafiknya :

Kosinus
Misalkan  , maka grafiknya
, maka grafiknya

Tangen
Misalkan , maka grafiknya
, maka grafiknya

3. Grafik fungsi  ;
; 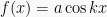 ; dan
; dan 
Didapat dari grafik trigonometri baku dengan cara mengalikan ordinat setiap titik pada grafik baku dengan bilangan a, sedangkan periode grafik sinus dan kosinus menjadi :

Dan tangen
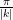
Misalkan  dan
dan 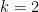 , maka grafiknya
, maka grafiknya

Misalkan  dan
dan 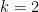 , maka grafiknya
, maka grafiknya

Misalkan a=1 dan k=3
dan k=3 , maka grafiknya
, maka grafiknya

4. Grafik fungsi  ;
;  ; dan
; dan  .
.
Didapat dari grafik trigonometri baku dengan cara mengalikan koordinat setiap titik pada grafik baku dengan bilangan a, sedangkan absisnya digeser sejauh :
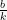
Jika b positif, absis digeser kekiri. Dan jika b negatif, absis digeser kekanan. Sedangkan periode grafik sinus dan kosinus menjadi :

Dan tangen
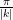
Misalkan  ,
, 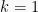 , dan
, dan  , maka grafiknya
, maka grafiknya

Misalkan  ,
, 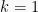 , dan
, dan  , maka grafiknya
, maka grafiknya

5. Grafik fungsi  ;
;  ; dan
; dan  .
.
Didapat dari grafik trigonometri baku dengan cara mengalikan koordinat setiap titik pada grafik baku dengan bilangan a, sedangkan absisnya digeser sejauh :
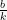
Jika b positif, absis digeser kekiri. Dan jika b negatif, absis digeser kekanan. Koordinat didapat dengan menggeser titik koordinat grafik baku keatas jika c positif dan kebawah jika c negatif. Sedangkan periode grafik sinus dan kosinus menjadi :

Dan tangen
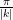
Misalkan  ,
, 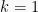 ,
,  , dan
, dan  maka grafiknya sinusnya:
maka grafiknya sinusnya:

Contoh Soal Grafik Fungsi Trigonometri dan Pembahasan
Contoh Soal 1
Fungsi  . Tentukan nilai maksimum, minimum, dan amplitudo fungsi tersebut.
. Tentukan nilai maksimum, minimum, dan amplitudo fungsi tersebut.
Pembahasan




Contoh Soal 2
Tentukan nilai maksimum dan minimum fungsi 
Pembahasan
Gunakan :
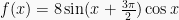


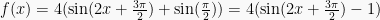

Sehingga :
- Untuk sin
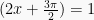 , maka
, maka 
- Untuk sin
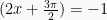 , maka
, maka 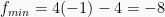
Contoh Soal 3
Bagilah sudut lancip α menjadi 2 bagian, sehingga hasil perkalian kosinus-kosinusnya mencapai nilai maksimum.
Tentukan nilai maksimum itu.
Pembahasan
Misalkan 2 bagian sudut adalah x dan α-x, maka f(x)=cosx cos(α-x). Berdasarkan rumus trigonometri  , maka :
, maka :


 akan maksimum jika
akan maksimum jika  , sehingga
, sehingga

Jika anda membutuhkan versi Audio Visual, anda bisa menonton tautan link Youtube di bawah:
jangan lupa isi absensi dan selesaikan tugas kalian, silahkan akses kelas masing-masing di classrom saya di tautan berikut:
XI MIPA 3
Link Tautan Kelas : https://classroom.google.com/c/MzcxNDQ3Mzk3MjY2?cjc=mzlmh6h
Kode Kelas : m z l m h 6 h
XI MIPA 4
Link Tautan Kelas : https://classroom.google.com/c/MjI2Mzg3MjU4NDQ1?cjc=4opp7aj
Kode Kelas : 4 o p p 7 a j
XI MIPA 7
Link Tautan Kelas : https://classroom.google.com/c/MjI2Mzg3Mjc0MDg1?cjc=cggrci5
Kode Kelas : c g g r c i 5
















