CONTOH SOAL DIMESI TIGA
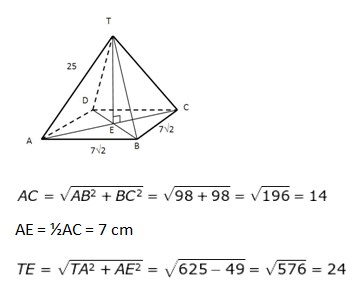
1. Pada limas beraturan T.ABCD, panjang rusuk tegaknya 25 cm dan panjang rusuk alasnya 7√2 cm. Jarak titik T ke bidang ABCD sama dengan …
Jawaban :
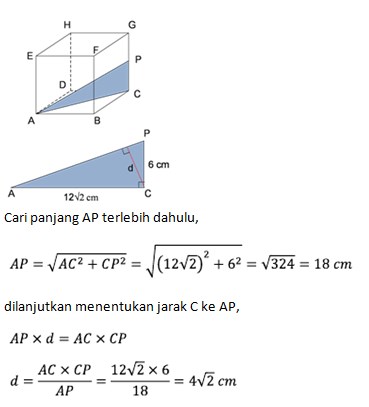
2. Pada kubus ABCD.EFGH dengan panjang rusuk 12 cm, titik P adalah tepat ditengah CG, tentukan jarak titik C ke garis AP!
Jawaban :
Posisi titik C dan garis AP pada kubus sebagai berikut:
3. Panjang rusuk kubus ABCD . EFGH adalah 6 cm. Jika S adalah titik potong EG dan FH, maka jarak DH ke AS adalah …
Jawaban :

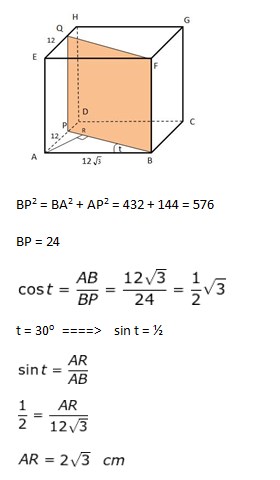
4. Pada kubus ABCDEFGH, titik P pada AD dan titik Q pada EH sehingga AP=EQ = 12 cm. Jika panjang rusuk 12√3 cm maka jarak A ke BPQF sama dengan …
Jawaban :
5. Kubus ABCD.EFGH dengan panjang sisi 12 cm. Titik P adalah perpotongan diagonal bidang ABCD. Tentukan jarak titik P ke titik G
Jawaban :
Gambar sebagai berikut
6. Perhatikan gambar kubus ABCD.EFGH. Jarak titik C dan bidang AFH

7. Bidang empat ABCD, pada gambar dengan AD tegak lurus alas. Sudut antara bidang BCD dan BCA adalah α, maka tan α
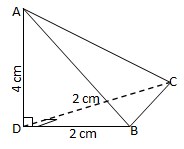
Jawaban :
8. Perhatikan gambar di bawah
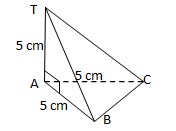
AT, AB dan AC saling tegak lurus di A. Jarak titik A ke bidang TBC adalah ….
Jawaban :

9. Pada kubus ABCD. EFGH, α adalah sudut antara bidang ADHE dan ACH. Nilai cos α = …
Jawaban :
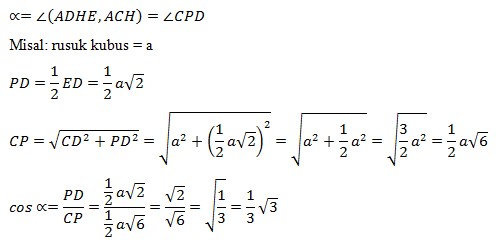
10. Diketahui kubus ABCD. EFGH, titik P,Q,R di pertengahan rusuk AD, BC, dan CG. Irisan bidang yang melalui P, Q dan R dengan kubus berbentuk ….
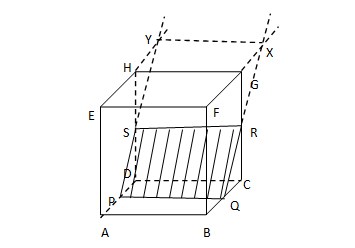
Jawaban :
Pada kubus ABCD.EFGH, titik P, Q, dan R terletak di pertengahan rusuk AD, BC, dan CG.
Langkah- langkah melukisnya adalah:
- Hubungkan titik P dan Q, karena keduanya terletak pada bidang ABCD. PQ adalah sumbu afinitas.
- Hubungkan titik Q dan R, karena keduanya terletak pada bidang BCGF.
- Perpanjang garis QR dan FG sehingga berpotongan di titik X.
- Perpanjang garis EH.
- Dari titik X buatlah garis yang sejajar HG sehingga memotong perpanjangan garis EH di titik Y.
- Hubungkan titik P dan Y sehingga memotong sisi DCGH di titik S.
Diperolehlah persegi panjang PQRS.
Jadi, irisan bidangnya berbentuk persegi panjang.
11. Diketahui kubus ABCD.EFGH dengan rusuk 8 cm. Panjang proyeksi DE pada BDHF adalah . . .
A. 2 √2 cm
B. 2 √6 cm
C. 4 √2 cm
D. 4 √6 cm
E. . 8 √2 cm
Jawaban :
Pembahasan :
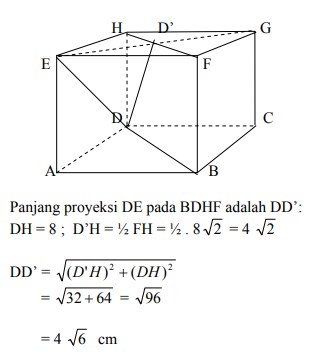
Jawabannya adalah D
12. Perhatikan gambar kubus ABCD.EFGH di bawah ini. Panjang proyeksi AF pada bidang ACGE adalah….
A. 6 √3 cm
B. 6 √2 cm
C. 3 √6 cm
D. 3 √3 cm
E. 3 √2 cm
Jawaban :
Pembahasan :
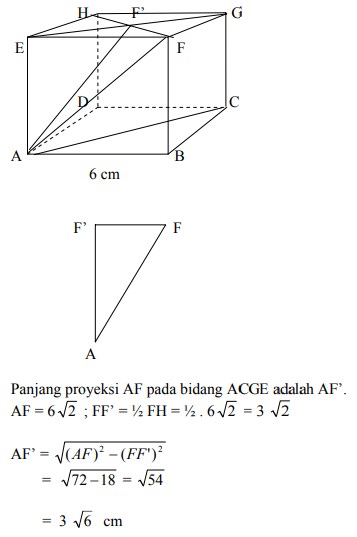
Jawabannya adalah C
13. Diketahui kubus ABCD.EFGH dengan rusuk 4 cm. Jika P titik tengah EH, maka jarak titik P ke garis CF adalah…
A. √20 cm
B. √18 cm
C. √14 cm
D. √12 cm
E. √8 cm
Jawaban : B
Pembahasan :
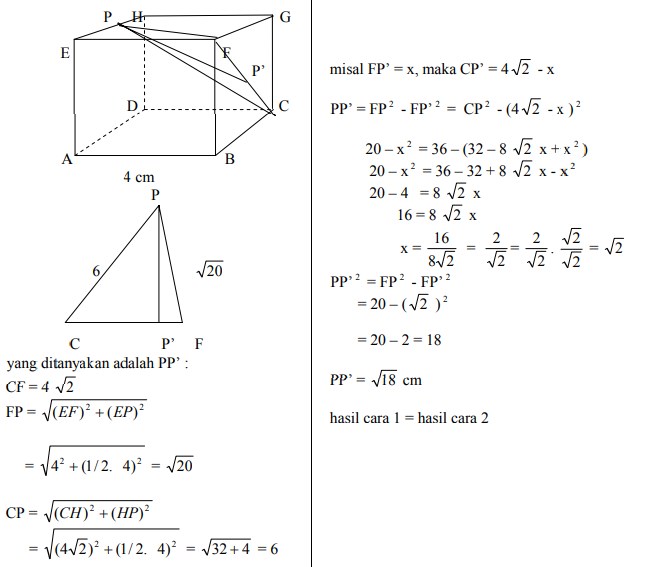
Jawabannya adalah B
14. Panjang rusuk kubus ABCD.EFGH adalah 6 cm. Jarak titik C dengan bidang BDG adalah…
A. 2√2 cm
B. 2√3 cm
C. 3√2 cm
D. 3√3 cm
E. 4√3 cm
Jawaban :
Pembahasan :
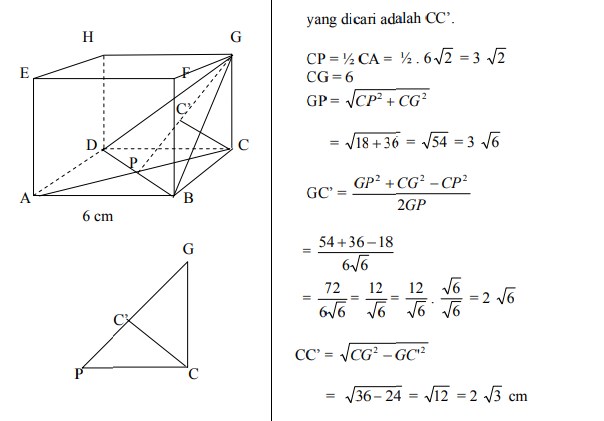
Jawabannya adalah B
15. Pada kubus ABCD.EFGH besar sudut antara garis AH dan bidang diagonal BDHF adalah…
A. 30°
B. 45°
C. 60°
D. 75°
E. 90°
Jawaban : A
Pembahasan :
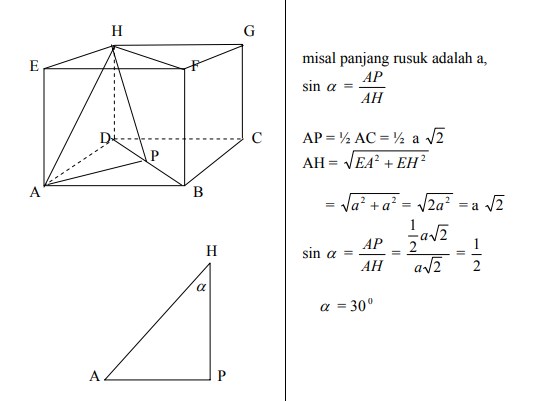
Jawabannya adalah A
16. Diketahui kubus ABCD.EFGH dengan rusuk 4 cm. Jika sudut antara BF dan bidang BEG adalah α , maka sin α = ….
A. ¼√2
B. ½√2
C. 1/3√3
D. ½√3
E. ½√6
Jawaban : C
Pembahasan :
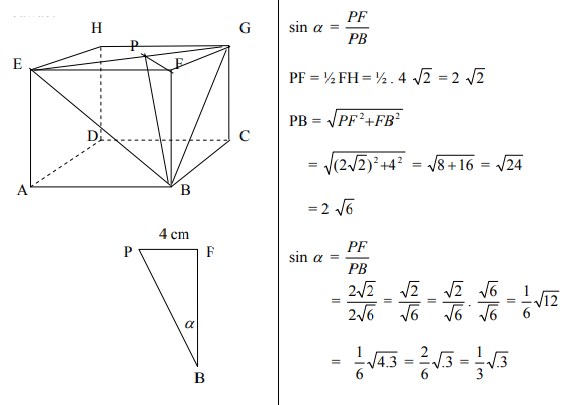
Jawabannya adalah C
17. Besar sudut antara diagonal BG dan FH pada kubus ABCD.EFGH adalah …..
A. 30°
B. 45°
C. 60°
D. 75°
E. 90°
Jawaban : C
Pembahasan :
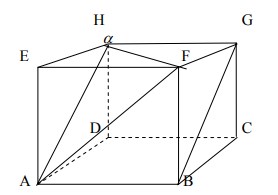
AH sejajar dengan BG, sehingga sudut antara diagonal BG dan FH adalah juga sudut antara diagonal AH dan FH (∠ (BG,FH) = ∠ (AH,FH) )
dari gambar terlihat bahwa panjang AH = AF = FH sehingga ∆ AFH adalah ∆sama sisi.
∆sama sisi. Mempunyai 3 sudut yang sama yaitu 60°
Jawabannya adalah C
18. Jarak bidang ACH dan EGB pada kubus ABCD.EFGH dengan rusuk 6 3 cm adalah….
A. 4 √3 cm
B. 2 √3 cm
C. 4 cm
D. 6 cm
E. 12 cm
Jawaban : D
Pembahasan :
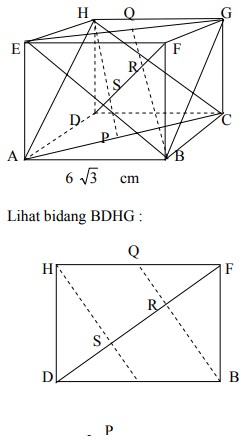
yang ditanya adalah jarak SR.
SR = DF – FR – DS
DF = 6 3 . 3 = 18 (diagonal ruang)
FR:
ingat titik berat ∆ = 1/3 tinggi
QR = 1/3 QB
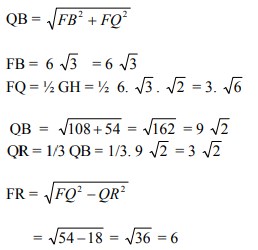
DS :
∆ DSP sebangun dengan ∆FQR
sehingga DS = FR = 6
Kita cari dan buktikan :
PS = 1/3 PH

Sehingga panjang SR = DF – FR – DS
= 18 – 6 – 6 = 6 cm
Jawabannya adalah D
19. Diketahui limas segitiga beraturan T.ABC. Panjang
rusuk AB= 6 cm, dan TA= 6√3 cm. Sudut antara TC dan bidang ABC adalah α , maka tan α = ….
A. 3√10
B. 4√2
C. 3√2
D. √10
E. 2√2
Jawaban : E
Pembahasan :
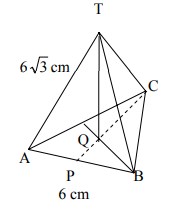
Karena limas segitiga beraturan maka:
panjang TA = TB = TC dan Bidangnya adalah segitiga sama sisi dengan panjang AB = BC = AC.
Sudut TC dan bidang ABC (∠TC, ABC) = ∠TCQ

Jawabannya adalah E
20. Pada limas segiempat beraturan T.ABCD yang semua rusuknya sama panjang. Sudut antara TA dan bidang ABCD adalah….
A. 15°
B. 30°
C. 45°
D. 60°
E. 75°
Jawaban : C
Pembahasan :
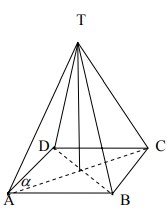
Misal panjang rusuk = a , maka
TA = TB = TB = TC = AB = BC = CD = AD = a
sudut antara TA dan bidang ABCD (∠ (TA,ABCD) ) adalah ∠ TAC

Jawabannya adalah C
Untuk mengisi absen, menyelesaikan tugas dan memulai diskusi silahkan masuk ke grup kelasnya masing-masing
XII MIPA 1
https://classroom.google.com/c/MTI4NzIyNzE5ODk4?cjc=qrtvm33
XII MIPA 2
https://classroom.google.com/c/MTI4NzIyNzE5OTIz?cjc=d62hyuv
XII MIPA 3
https://classroom.google.com/c/MTE2OTk2MDYzNTc1?cjc=sir5vrf
XII MIPA 4
https://classroom.google.com/c/MTE2OTk2MDYzNTgy?cjc=ultb4pg
XII MIPA 5
https://classroom.google.com/c/MTE2OTk2MDYzNTg4?cjc=g4ykrog
XII MIPA 6
https://classroom.google.com/c/MTE2OTk2MDYzNjAx?cjc=ed6boyy
XII MIPA 7
https://classroom.google.com/c/MTE2OTk2MDYzNjEw?cjc=gapjtqi


Tidak ada komentar:
Posting Komentar