Contoh Soal Teorema Phytagora (31/01/2021)

Pada kesempatan ini, ID-KU memposting Soal Penerapan Teorema Pythagoras dalam Kehidupan. Dalam kehidupan nyata, banyak permasalahan sehari-hari yang dapat diselesaikan dengan menggunakan teorema pythagoras. Berikut beberapa kumpulan soal penerapan teorema pythagoras dalam kehidupan.

Soal Penerapan Teorema Pythagoras

Soal ❶ (UN Matematika SMP 2016)

Sebuah kapal berlayar sejauh 100 km ke arah barat, kemudian berbelok ke arah selatan sejauh 75 km. Jarak terpendek kapal tersebut dari titik keberangkatan adalah ….

A.  75 km
B.  100 km
C.  125 km
D.  175 km

Pembahasan:
Perhatikan gambar di bawah.

Jarak terpendek kapal tersebut dari titik keberangkatan dapat dicari dengan menggunakan teorema pythagoras.
Jarak = 1002+752−−−−−−−−−√
         = 10.000+5.625−−−−−−−−−−−−√
         = 15.625−−−−−√
         = 125
Jadi, jarak terpendek kapal tersebut dari titik keberangkatan adalah 125 km.
(Jawaban: C)

Soal ❷ (UN Matematika SMP 2016)
Sebuah tiang tingginya 12 m berdiri tegak di atas tanah datar. Dari ujung atas tiang ditarik seutas tali ke sebuah patok pada tanah. Jika panjang tali 15 m, maka jarak patok dengan pangkal tiang bagian bawah adalah ….
A. 13,5 m
B. 10 m
C. 9 m
D. 3 m

Pembahasan:
Soal di atas dapat digambarkan seperti pada gambar di bawah.

 

Jarak patok dengan pangkal tiang bagian bawah dapat dicari dengan menggunakan teorema pythagoras:
Jarak = 152−122−−−−−−−−√
         = 225−144−−−−−−−−√
         = 81−−√
         = 9
(Jawaban: C)

Soal ❸

Sebuah tangga yang panjangnya 5 meter bersandar pada pohon. Jarak  ujung bawah tangga terhadap pohon = 3 meter. Hitunglah tinggi pohon yang dapat dicapai oleh tangga.

Pembahasan:
Perhatikan gambar berikut:

Berdasarkan gambar di atas, tinggi pohon dapat dicari dengan menggunakan teorema pythagoras.
Tinggi = 52−32−−−−−−√
           = 25−9−−−−−√
           = 16−−√
           = 4
Jadi, tinggi pohon yang dapat dicapai oleh tangga adalah  4 meter.

Soal ❹

Seorang anak menaikkan layang-layang dengan benang yang panjangnya 120 meter. Jarak kaki anak dengan permukaan tanah yang berada tepat di bawah layang-layang adalah 40 meter.  Hitunglah tinggi layang-layang tersebut jika tinggi tangan yang memegang ujung benang berada 1,2 meter di  atas permukaan tanah! (Benang dianggap lurus)

Pembahasan:
Perhatikan gambar berikut:

Dengan menggunakan teorema pythagoras, maka tinggi (t):
Tinggi = 1202−402−−−−−−−−−√
           = 14.400−1.600−−−−−−−−−−−−√
           = 12.800−−−−−√
           = 113,1
Tinggi layang-layang = 113,1 + 1,2 = 114,3
Jadi, tinggi layang-layang tersebut adalah 114,3 meter.

Soal ❺

Seorang anak akan mengambil sebuah layang-layang yang tersangkut di atas sebuah tembok yang berbatasan langsung dengan sebuah kali. Anak tersebut ingin menggunakan sebuah tangga untuk mengambil layang-layang tersebut dengan cara meletakan kaki tangga di pinggir kali. Jika lebar kali tersebut 5 meter dan tinggi tembok 12 meter, hitunglah panjang tangga minimal yang diperlukan agar ujung tangga bertemu dengan bagian atas tembok
Pembahasan:
Perhatikan  gambar di bawah.
BC adalah tinggi tembok, BC = 12 m
AB adalah lebar kali, AB = 5 m.
AC adalah panjang tangga.

Dengan menggunakan teorema pythagoras, maka panjang tangga minimal:
AC = 122+52−−−−−−−√
      = 144+25−−−−−−−√
      = 169−−−√
      = 13
Jadi, panjang tangga minimal yang diperlukan agar ujung tangga bertemu dengan bagian atas tembok adalah 13 meter.

Soal ❻

Dua buah tiang berdampingan berjarak 24 m. Jika tinggi tiang masing-masing adalah 22 m dan 12 m, hitunglah panjang kawat penghubung antara ujung tiang tersebut.

Pembahasan:
Pehatikan  gambar berikut:

A merupakan tiang pertama dengan tinggi 12 meter dan B merupakan  tiang kedua dengan tinggi 22  meter. AB merupakan panjang kawat penghubung antara tiang A dan tiang B. Dengan menggunakan  teorema pythagoras, panjang kawat penghubung kedua tiang:

AB = AC2+BC2−−−−−−−−−−√
      = 242+(22−12)2−−−−−−−−−−−−−√
      = 242+102−−−−−−−−√
      = 576+100−−−−−−−−√
      = 676−−−√
      = 26
Jadi, panjang kawat penghubung antara ujung tiang tersebut adalah 26 meter

Soal ❼

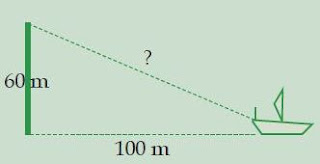
Seorang nakhoda kapal melihat pun cak mercusuar yang berjarak 100 meter dari kapal. Jika diketahui tinggi mercusuar 60 meter, tentukan jarak nakhoda dari puncak mercusuar tersebut!

Pembahasan:
Perhatikan gambar berikut:

Dengan menggunakan teorema pythagoras, maka jarak nakhoda dari puncak mercusuar:
Jarak = 1002+602−−−−−−−−−√
      = 10.000+3.600−−−−−−−−−−−−√
      = 13.600−−−−−√
      = 116,62

Jadi, jarak nakhoda dari puncak mercusuar tersebut adalah 116,62 meter.

TUGAS DAN ABSENSI

Setelah kalian simak pembahasan di atas, silahkan catatan dalam buku tulis dan dikumpulkan ketika luring/ tatap muka oleh guru kalian

untuk Absensi Silahkan isi di bawah: